Writeup: HackCon 2019 - AgainAndAgainAndAgain

(Updated: )
writeups
, , , ,

Information

  • category : crypto
  • points : 467

Description

Someone was thinking encrypting again and again helps, prove them wrong.

c = 196353764385075548782571270052469419021844481625366305056739966550926484027148967165867708531585849658610359148759560853

File : q1.py

Writeup

Content of q1.py :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def encrypt(m):
	return pow(m,2,n)

p = 5411451825594838998340467286736301586172550389366579819551237
q = 5190863621109915362542582192103708448607732254433829935869841

n = p*q

flag = int('d4rk{*************REDACTED!!!!!!************}code'.encode('hex'),16)

l = encrypt(flag)
while l > flag:
    l = encrypt(l)
print(l)

We have : n = p * q, p, q, c. To encrypt a message m the script does : (m ^ 2) % n = c.

The encryption remembers RSA, however in this case we have e = 2 which is not a possible exponent in RSA because gcd(2, phi(n)) = 2 and so the inverse of e in phi(n) is not possible. This cryptosystem with exponent 2 is the Rabin cryptosystem.

Decrypting a ciphertext c we get 4 different results. To decrypt we need to:

    • Compute mp = c ^ (1/4 * (p + 1)) mod p
      • Compute mq = c ^ (1/4 * (q + 1)) mod q
      • Both can be expressed as :
  • Use Extended Euclidean algorithm to find yp and yq s.t. yp * p + yq * q = gcd(p, q) = 1
  • Use the Chinese remainder theorem to find the fours square roots of c mod n :
    • r1 = (yp * p * mq + yq * q * mp) mod n
    • r2 = n - r1
    • r3 = (yp * p * mq - yq * q * mq) mod n
    • r4 = n - r3

Difficulty

During encryption the challenger encrypts the flag n times, we don’t know how many times (n) because we don’t know the flag. To solve the problem we can imagine the following graph :

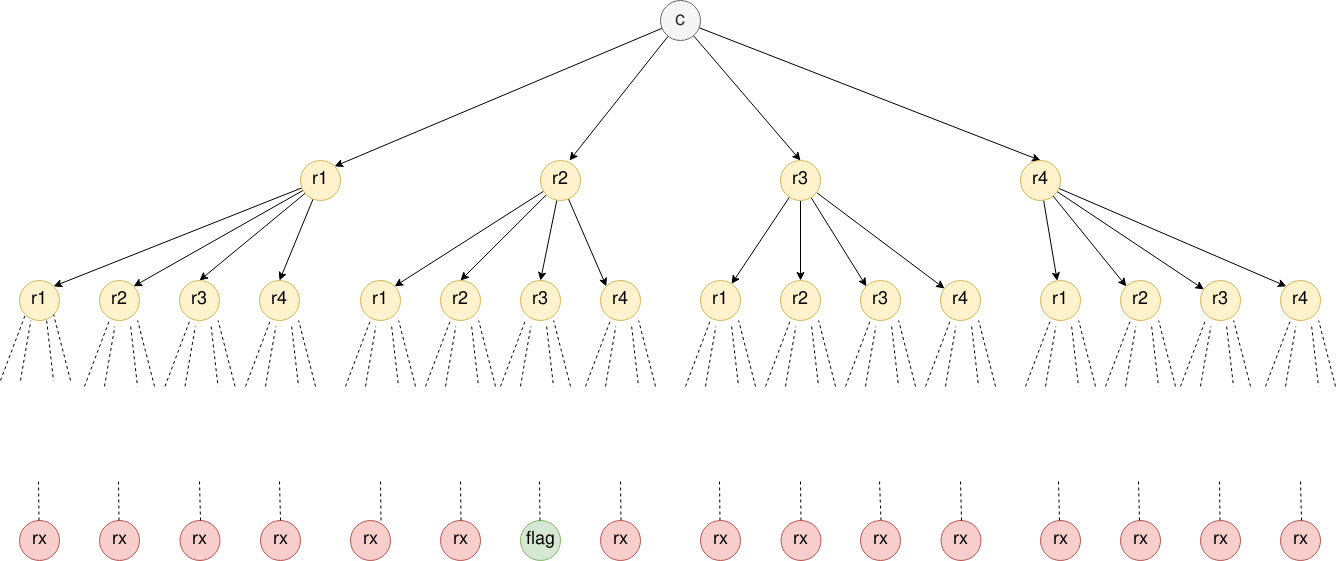
Where recursively during the decryption we create 4 times more nodes at each level. In the level i there will be 4^i nodes.

To solve this problem we can implement a BFS. Implementing a DFS is not a valid approach. We don’t have the graph structure and we need to create one on the fly, with a DFS we don’t know where to stop “searching”.

BFS pseudocode:

1
2
3
4
5
6
7
8
9
10
11
12
13
procedure BFS(G,start_v):
    let Q be a queue
    label start_v as discovered
    Q.enqueue(start_v)
    while Q is not empty
        v = Q.dequeue()
        if v is the goal:
            return v
        for all edges from v to w in G.adjacentEdges(v) do
            if w is not labeled as discovered:
                label w as discovered
                w.parent = v
                Q.enqueue(w)

Exploit

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#!/usr/bin/env python3
from modsqrt import modular_sqrt 
# Taken from :
# https://gist.githubusercontent.com/nakov/60d62bdf4067ea72b7832ce9f71ae079/raw/864c0eb6e58329db8444a7a6fc3df28c0fc8580f/modsqrt.py
from Crypto.Util.number import long_to_bytes

p = 5411451825594838998340467286736301586172550389366579819551237
q = 5190863621109915362542582192103708448607732254433829935869841
n = p * q

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def bfs(ct):
    # Define queue
    queue = []
    queue.append(ct)
    while len(queue) != 0:
        # Pop element from queue 
        v = queue.pop(0)
        # Check if it's the right one
        if b'd4rk{' in long_to_bytes(v):
            print(long_to_bytes(v))
            exit(0)
        # Computes...
        mp = modular_sqrt(v, p)
        mq = modular_sqrt(v, q)
        g, yp, yq = egcd(p, q)
        r1 = (yp * p * mq + yq * q * mp) % n
        r2 = n - r1
        r3 = (yp * p * mq - yq * q * mp) % n 
        r4 = n - r3
        possible_pt = [r1, r2, r3, r4]
        # Enqueue
        for pt in possible_pt:
            if not pt in queue:
                queue.append(pt)

def main():
    c = 196353764385075548782571270052469419021844481625366305056739966550926484027148967165867708531585849658610359148759560853
    bfs(c)

if __name__ == '__main__':
    main()

Flag

d4rk{r3p3t1t1v3_r4b1n_1s_th4_w0rs7_3vaaaaaar!}code