Writeup: Sharky CTF 2020 - Z3 Robot

Information

• category : reverse
• points : 188

Description

I made a robot that can only communicate with “z3”. He locked himself and now he is asking me for a password !

1 file: z3_robot

Writeup

We’re given a file named z3_robot.

$ file z3_robot 
z3_robot: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2,
for GNU/Linux 3.2.0, BuildID[sha1]=bce2975b632a64a4c4af2009a81f41f43619dad1, not stripped

So it’s an ELF binary, 64 bit not stripped. If we run it we get the following message:

      \_/
     (* *)
    __)#(__
   ( )...( )(_)
   || |_| ||//
>==() | | ()/
    _(___)_
   [-]   [-]   Z3 robot says :z3 Z3Z3z3 Zz3 zz33 3Z Passz3rd? Zz3 zZ3 3Z Z3Z3z
-> # WAITING FOR INPUT HERE

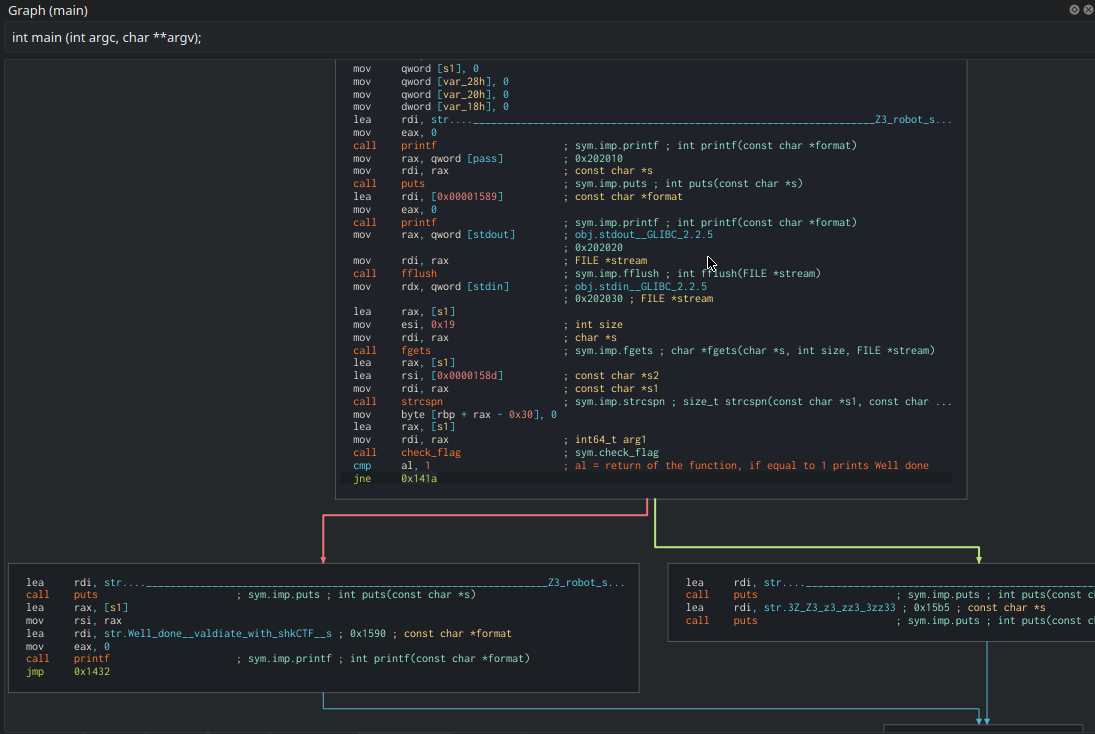
So I opened it with Cutter and I started analyzing main:

The main read our input with fgets and then pass it as argument to check_flag.
If check_flag function returns 1, the challenge is solved.

The graph overview of check_flag is the following (not very short):

Now let’s see the decompiled of check_flag (with r2ghidra-dec):

// Cleaned version
undefined8 check_flag(int64_t arg1)
{
    undefined8 uVar1;
    uint8_t uVar2;
    int64_t var_8h;
    if (((((*(arg1 + 0x14) ^ 0x2b) == *(arg1 + 7)) &&
               (*(arg1 + 0x15) - *(arg1 + 3) == -0x14)) &&
              (*(arg1 + 2) >> 6 == '\0')) &&
             ((*(arg1 + 0xd) == 't' && ((*(arg1 + 0xb) & 0x3fffffffU) == 0x5f)))) &&
            ((uVar2 = (*(arg1 + 0x11) >> 7) >> 5,
             *(arg1 + 7) >> ((*(arg1 + 0x11) + uVar2 & 7) - uVar2 & 0x1f) == 5 &&
             (((*(arg1 + 6) ^ 0x53) == *(arg1 + 0xe) && (*(arg1 + 8) == 'z')))))) &&
           ((uVar2 = (*(arg1 + 9) >> 7) >> 5,
            *(arg1 + 5) << ((*(arg1 + 9) + uVar2 & 7) - uVar2 & 0x1f) == 0x188 &&
            ((((*(arg1 + 0x10) - *(arg1 + 7) == 0x14 &&
               (uVar2 = (*(arg1 + 0x17) >> 7) >> 5,
               *(arg1 + 7) << ((*(arg1 + 0x17) + uVar2 & 7) - uVar2 & 0x1f) == 0xbe)) &&

                // MANY MORE LINES OF CONSTRAINTS

               (uVar2 = (*(arg1 + 0x16) >> 7) >> 5,
               *(arg1 + 7) << ((*(arg1 + 0x16) + uVar2 & 7) - uVar2 & 0x1f) == 0x17c)) &&
              (*(arg1 + 0x16) == ':')) &&
             ((*(arg1 + 0x10) == 's' && ((*(arg1 + 0x17) ^ 0x1d) == *(arg1 + 0x12)))))))))
          )))) && (((*(arg1 + 0xe) + *(arg1 + 0x17) == 0x59 &&
                    (((*(arg1 + 2) & *(arg1 + 5)) == 0x30 &&
                     ((*(arg1 + 0xf) & 0x9fU) == 0x1f)))) &&
                   ((*(arg1 + 4) == 's' &&
                    (((*(arg1 + 0x17) ^ 0x4a) == *arg1 &&
                     ((*(arg1 + 6) ^ 0x3c) == *(arg1 + 0xb))))) {
        uVar1 = 1;
    } else {
        uVar1 = 0;
    }
    return uVar1;
}

To solve the challenge we have to make all the constraints inside the if true.

There are two possible ways to solve those constraints:

1. angr
2. z3

Angr Solution

The main issues an fgets of 0x19 (25) bytes, so our input must be of that dimension.

proj = angr.Project("z3_robot",load_options={"auto_load_libs": False},
                    main_opts={"base_addr": 0})
flag = [claripy.BVS(f"c_{i}", 8) for i in range(0x19)]
flag_ast = claripy.Concat(*flag)
state = proj.factory.entry_state(stdin=flag_ast)

We add the constraints that makes the flag readable:

for f in flag:
    state.solver.add(f >= 0x20)
    state.solver.add(f < 0x7f)

Then we launch the exploration to find in the stdout the string “Well done”:

simgr = proj.factory.simulation_manager(state)
print("start exploring")
simgr.explore(find=lambda s: b"Well" in s.posix.dumps(1))

And finally:

found = simgr.found[0]
valid_flag = found.solver.eval(flag_ast, cast_to=bytes)
print(valid_flag)

The final exploit is:

#!/usr/bin/env python3

import angr 
import claripy

proj = angr.Project("z3_robot",load_options={"auto_load_libs": False},
                    main_opts={"base_addr": 0})
flag = [claripy.BVS(f"c_{i}", 8) for i in range(0x19)]
flag_ast = claripy.Concat(*flag)
state = proj.factory.entry_state(stdin=flag_ast)
for f in flag:
    state.solver.add(f >= 0x20)
    state.solver.add(f < 0x7f)

simgr = proj.factory.simulation_manager(state)
print("start exploring")
simgr.explore(find=lambda s: b"Well" in s.posix.dumps(1))

if len(simgr.found) > 0:
    found = simgr.found[0]
    valid_flag = found.solver.eval(flag_ast, cast_to=bytes)
    print(valid_flag)
else:
    print("unlucky")

Z3 Solution

Another way to solve the challenge is to use z3.

Since the ghidra’s decompiled of check_flag is a bit messy we can use the IDA’s one, which is more polished:

return ((unsigned __int8)a1[20] ^ 0x2B) == a1[7]
      && a1[21] - a1[3] == -20
      && !(a1[2] >> 6)
      && a1[13] == 116
      && 4 * a1[11] == 380
      && a1[7] >> (a1[17] % 8) == 5
      && ((unsigned __int8)a1[6] ^ 0x53) == a1[14]
      && a1[8] == 122
      && a1[5] << (a1[9] % 8) == 392
      && a1[16] - a1[7] == 20
      && a1[7] << (a1[23] % 8) == 190
      && a1[2] - a1[7] == -43
      && a1[21] == 95
      && ((unsigned __int8)a1[2] ^ 0x47) == a1[3]
      && *a1 == 99
      && a1[13] == 116
      && (a1[20] & 0x45) == 68
      && (a1[8] & 0x15) == 16
      && a1[12] == 95
      && a1[4] >> 4 == 7
      && a1[13] == 116
      && *a1 >> (*a1 % 8) == 12
      && a1[10] == 95
      && (a1[8] & 0xAC) == 40
      && a1[16] == 115
      && (a1[22] & 0x1D) == 24
      && a1[9] == 51
      && a1[5] == 49
      && 4 * a1[19] == 456
      && a1[20] >> 6 == 1
      && a1[7] >> 1 == 47
      && a1[1] == 108
      && a1[3] >> 4 == 7
      && (a1[19] & 0x49) == 64
      && a1[4] == 115
      && ((unsigned __int8)a1[2] & (unsigned __int8)a1[11]) == 20
      && *a1 == 99
      && a1[4] + a1[5] == 164
      && a1[15] << 6 == 6080
      && ((unsigned __int8)a1[10] ^ 0x2B) == a1[17]
      && ((unsigned __int8)a1[12] ^ 0x2C) == a1[4]
      && a1[19] - a1[21] == 19
      && a1[12] == 95
      && a1[15] >> 1 == 47
      && a1[19] == 114
      && a1[17] + a1[18] == 168
      && a1[22] == 58
      && ((unsigned __int8)a1[23] & (unsigned __int8)a1[21]) == 9
      && a1[6] << (a1[19] % 8) == 396
      && a1[3] + a1[7] == 210
      && (a1[22] & 0xED) == 40
      && (a1[12] & 0xAC) == 12
      && ((unsigned __int8)a1[18] ^ 0x6B) == a1[15]
      && (a1[16] & 0x7A) == 114
      && (*a1 & 0x39) == 33
      && ((unsigned __int8)a1[6] ^ 0x3C) == a1[21]
      && a1[20] == 116
      && a1[19] == 114
      && a1[12] == 95
      && a1[2] == 52
      && a1[23] == 41
      && a1[10] == 95
      && ((unsigned __int8)a1[22] & (unsigned __int8)a1[9]) == 50
      && a1[3] + a1[2] == 167
      && a1[17] - a1[14] == 68
      && a1[21] == 95
      && ((unsigned __int8)a1[19] ^ 0x2D) == a1[10]
      && 4 * a1[12] == 380
      && a1[6] & 0x40
      && ((unsigned __int8)a1[12] & (unsigned __int8)a1[22]) == 26
      && a1[7] << (a1[19] % 8) == 380
      && ((unsigned __int8)a1[20] ^ 0x4E) == a1[22]
      && a1[6] == 99
      && a1[12] == a1[7]
      && a1[19] - a1[13] == -2
      && a1[14] >> 4 == 3
      && (a1[12] & 0x38) == 24
      && a1[8] << (a1[10] % 8) == 15616
      && a1[20] == 116
      && a1[6] >> (a1[22] % 8) == 24
      && a1[22] - a1[5] == 9
      && a1[7] << (a1[22] % 8) == 380
      && a1[22] == 58
      && a1[16] == 115
      && ((unsigned __int8)a1[23] ^ 0x1D) == a1[18]
      && a1[23] + a1[14] == 89
      && ((unsigned __int8)a1[5] & (unsigned __int8)a1[2]) == 48
      && (a1[15] & 0x9F) == 31
      && a1[4] == 115
      && ((unsigned __int8)a1[23] ^ 0x4A) == *a1
      && ((unsigned __int8)a1[6] ^ 0x3C) == a1[11];

What we need to do is:

• remove the casting to (unsigned __int8).
• change the pointer to the first element of the array *a1 to a1[0].
• need to adapts the bit a bit operations a bit (:D).

Final exploit:

#!/usr/bin/env python3

from z3 import *

# List of BitVec
a1 = [BitVec(f'{i}', 8) for i in range(0x19)]
s = Solver()

# Constraints
s.add((a1[20] ^ 0x2B) == a1[7])
s.add(a1[21] - a1[3] == -20)
s.add((a1[2] >> 6) == 0)
s.add(a1[13] == 116)
s.add(4 * a1[11] == 380)
s.add(a1[7] >> (a1[17] % 8) == 5)                
s.add((a1[6] ^ 0x53) == a1[14])
s.add(a1[8] == 122)
s.add(a1[5] << (a1[9] % 8) == 392)
s.add(a1[16] - a1[7] == 20)
s.add(a1[7] << (a1[23] % 8) == 190)
s.add(a1[2] - a1[7] == -43)
s.add(a1[21] == 95)
s.add((a1[2] ^ 0x47) == a1[3])
s.add(a1[0] == 99)
s.add(a1[13] == 116)
s.add((a1[20] & 0x45) == 68)
s.add((a1[8] & 0x15) == 16)
s.add(a1[12] == 95)
s.add(a1[4] >> 4 == 7)
s.add(a1[13] == 116)
s.add(a1[0] >> (a1[0] % 8) == 12)
s.add(a1[10] == 95)
s.add((a1[8] & 0xAC) == 40)
s.add(a1[16] == 115)
s.add((a1[22] & 0x1D) == 24)
s.add(a1[9] == 51)
s.add(a1[5] == 49)
s.add(4 * a1[19] == 456)
s.add(a1[20] >> 6 == 1)
s.add(a1[7] >> 1 == 47)
s.add(a1[1] == 108)
s.add(a1[3] >> 4 == 7)
s.add((a1[19] & 0x49) == 64)
s.add(a1[4] == 115)
s.add(a1[2] & a1[11] == 20)
s.add(a1[0] == 99)
s.add(a1[4] + a1[5] == 164)
s.add(a1[15] << 6 == 6080)
s.add(a1[10] ^ 0x2B == a1[17])
s.add(a1[12] ^ 0x2C == a1[4])
s.add(a1[19] - a1[21] == 19)
s.add(a1[12] == 95)
s.add(a1[15] >> 1 == 47)
s.add(a1[19] == 114)
s.add(a1[17] + a1[18] == 168)
s.add(a1[22] == 58)
s.add(a1[23] & a1[21] == 9)
s.add(a1[6] << (a1[19] % 8) == 396)
s.add(a1[3] + a1[7] == 210)
s.add((a1[22] & 0xED) == 40)
s.add((a1[12] & 0xAC) == 12)
s.add((a1[18] ^ 0x6B) == a1[15])
s.add((a1[16] & 0x7A) == 114)
s.add((a1[0] & 0x39) == 33)
s.add((a1[6] ^ 0x3C) == a1[21])
s.add(a1[20] == 116)
s.add(a1[19] == 114)
s.add(a1[12] == 95)
s.add(a1[2] == 52)
s.add(a1[23] == 41)
s.add(a1[10] == 95)
s.add((a1[22] & a1[9]) == 50)
s.add(a1[3] + a1[2] == 167)
s.add(a1[17] - a1[14] == 68)
s.add(a1[21] == 95)
s.add((a1[19] ^ 0x2D) == a1[10])
s.add(4 * a1[12] == 380)
s.add(a1[6] & 0x40 >= 1)
s.add((a1[12] & a1[22]) == 26)
s.add(a1[7] << (a1[19] % 8) == 380)
s.add((a1[20] ^ 0x4E) == a1[22])
s.add(a1[6] == 99)
s.add(a1[12] == a1[7])
s.add(a1[19] - a1[13] == -2)
s.add(a1[14] >> 4 == 3)
s.add((a1[12] & 0x38) == 24)
s.add(a1[8] << (a1[10] % 8) == 15616)
s.add(a1[20] == 116)
s.add(a1[6] >> (a1[22] % 8) == 24)
s.add(a1[22] - a1[5] == 9)
s.add(a1[7] << (a1[22] % 8) == 380)
s.add(a1[22] == 58)
s.add(a1[16] == 115)
s.add((a1[23] ^ 0x1D) == a1[18])
s.add(a1[23] + a1[14] == 89)
s.add((a1[5] & a1[2]) == 48)
s.add((a1[15] & 0x9F) == 31)
s.add(a1[4] == 115)
s.add((a1[23] ^ 0x4A) == a1[0])
s.add((a1[6] ^ 0x3C) == a1[11])

print(s.check())
model = s.model()
flag = ''.join([chr(int(str(model[a1[i]]))) for i in range(len(model))])
print(flag)

$ ./z3_robot 
      \_/
     (* *)
    __)#(__
   ( )...( )(_)
   || |_| ||//
>==() | | ()/
    _(___)_
   [-]   [-]   Z3 robot says :z3 Z3Z3z3 Zz3 zz33 3Z Passz3rd? Zz3 zZ3 3Z Z3Z3z
-> cl4ss1c_z3___t0_st4rt_:)
      \_/
     (* *)
    __)#(__
   ( )...( )(_)
   || |_| ||//
>==() | | ()/
    _(___)_
   [-]   [-]   Z3 robot says :
Well done, valdiate with shkCTF{cl4ss1c_z3___t0_st4rt_:)}

Flag

shkCTF{cl4ss1c_z3___t0_st4rt_:)}